relaciones y funciones

  RESEÑA HISTORICA 

El concepto de función como un objeto matemático independiente, susceptible de ser estudiado por sí solo, no apareció hasta los inicios del calculo en el siglo XVII.  René Descartes, Isaac Newton y Gottfried Leibniz establecieron la idea de función como dependencia entre dos cantidades variables. Leibniz en particular acuñó los términos «función», «variable», «constante» y «parámetro». La notación f (x) fue utilizada por primera vez por A.C. Clairaut, y por Leonhard Euler en su obra Commentarii de San petersburgo en 1736.

La primera función

El primero en construir una función fue Galileo (1564- 1642). Desde lo alto de la torre inclinada de Pisa tiró dos bolas, una de hierro y otra de madera y comprobó que a pesar de la diferencia de peso, ambas llegaban al suelo a la vez, había descubierto la ley de caída de los cuerpos.

Continuando su estudio y empleando un curioso artilugio, comprobó que el espacio recorrido depende del cuadrado del tiempo, escribiendo la primera función de la historia.

La primera definición formal de función se debe a Euler, quien en el libro Introductio in analysis infinitorum, publicado en 1748, dice:

“Una función de una cantidad variable es una expresión analítica compuesta de cualquier manera a partir de la cantidad variable y de números o cantidades constantes”.

En 1755 en Institutiones calculi differentialis, vuelve sobre el tema acercándose más a la que hoy utilizamos.

En base a lo comentado, investigue y desarrolle una línea de tiempo para la función matemática, destacando representantes y acontecimientos; por ejemplo Leonhard Euler en 1748 da la primera definición formal de función.

Par ordenado

En matemáticas, un par ordenado es una pareja de objetos matemáticos, en la que se distingue un primer elemento y un segundo elemento. El par ordenado cuyo primer elemento es a y cuyo segundo elemento es b se denota como (a, b).
Un par ordenado (a, b) no es el conjunto que contiene a a y b, denotado por {a, b}. Un conjunto está definido únicamente por sus elementos, mientras que en un par ordenado el orden de estos es también parte de su definición. Por ejemplo, los conjuntos {0, 1} y {1, 0} son idénticos, pero los pares ordenados (0, 1) y (1, 0) son distintos.
Los pares ordenados también se denominan 2-tuplas o vectores 2-dimensionales. La noción de una colección finita de objetos ordenada puede generalizarse a más de dos objetos, dando lugar al concepto de n-tupla.
El producto cartesiano de conjuntos, las relaciones binarias, las coordenadas cartesianas, las fracciones y las funciones se definen en términos de pares ordenados.

Producto cartesiano

En matemáticas, el producto cartesiano de dos conjuntos es una operación, que resulta en otro conjunto, cuyos elementos son todos los pares ordenados que pueden formarse tomando el primer elemento del par ordenado del primer conjunto y el segundo elemento del par ordenado del segundo conjunto.
Por ejemplo, dados los conjuntos:

   A =   {1, 2, 3, 4}

y
            B =   {a,b}

su producto cartesiano es:   

que se representa:
       A x B =   { (1, a), (1, b), (2, a), (2, b), (3, a), (3, b), (4, a), (4, b) }

  relacion 

v

una relación establece  la correspondencia entre los elementos de un conjunto no vació

 A y B . Generalmente  al conjunto A se lo llama conjunto de partida y al conjunto B conjunto de llegada  simbólicamente  se lo representa .

R ⊆ AXB

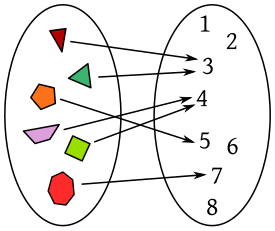
Dominio de una Relación

Dada una relación construida a partir de los conjuntos A y B los elementos del conjunto A que establecen correspondencia constituyen  el dominio de la relación.se lo representa Dom R.

   

Rango de una Relación 

Dada una relación construida a partir  de los conjuntos  A y B .Loa elementos del conjunto B que se relacionan con los elementos del dominio de R .constituye el rango de una relación   .

FUNCIÓN 

Una relación de A y B es una función si y solo si el dominio de la relación  es todo el conjunto de partida y si a cada elemento del dominio le corresponde un único  elemento de rango.

FUNCIONES DE VARIABLE REAL 

DOMINIO DE LA FUNCIÓN

Sea F una función de variable real ,el conjunto x para  el que  se encuentra  definido constituye el dominio de la función.

Consideraciones  

-Cuando sea un cociente  que el denominador , si hay  X nunca se haga cero .

-cuando tenga  una raíz de indice par debo tomar en cuenta  de que no sea negativa. 

RANGO  DE LA FUNCIÓN

Sea  F una función de variable real ,el conjunto de todas las imágenes de los elementos del dominio constituye el rango de la función.se representa simbólicamente Rg f.

Pasos 

-Despejar X 

-El rango sera el conjunto de valores que tome la variable Y.

REPRESENTACIÓN GRÁFICA DE UNA  FUNCIÓN

A cada X le pertenece un solo Y .

si F es una función de A en B entonces la gráfica de F es el conjunto de pares ordenados de A en B tales que su coordenada son (x,y). 

CRITERIO DE LA RECTA VERTICAL 

Si cualquier recta  vertical intersecta la gráfica en un solo punto es función.

si hay dos puntos al interceptar la recta es relación

TIPOS DE FUNCIONES 

Inyectivo

Injectivo" significa que cada elemento de "B" tiene como mucho uno de "A" al que corresponde (pero esto no nos dice que todos los elementos de "B" tengan alguno en "A").

Ejemplo: f(x) = x² del conjunto de los números naturales  a  es una función inyectiva.

(Pero f(x) = x² no es inyectiva cuando es desde el conjunto de enteros  (esto incluye números negativos) porque tienes por ejemplo

• f(2) = 4 y
• f(-2) = 4)

Nota: inyectiva también se llama "uno a uno", pero esto se confunde porque suena un poco como si fuera biyectiva.

Sobreyectivo (o también "epiyectivo")

Una función f (de un conjunto A a otro B) es sobreyectiva si para cada y en B, existe por lo menos un x en Aque cumple f(x) = y, en otras palabras f es sobreyectiva si y sólo si f(A) = B.

Así que cada elemento de la imagen corresponde con un elemento del dominio por lo menos.

Ejemplo: la función f(x) = 2x del conjunto de los números naturales  al de los números pares no negativos es sobreyectiva.

Sin embargo, f(x) = 2x del conjunto de los números naturales  a  no es sobreyectiva, porque, por ejemplo, ningún elemento de  va al 3 por esta función.

Biyectiva

"Biyectivo" significa inyectivo y sobreyectivo a la vez. Así que hay una correspondencia perfecta "uno a uno" entre los elementos de los dos conjuntos.

Ejemplo: La función f(x) = x² del conjunto de números reales positivos al mismo conjunto es inyectiva y sobreyectiva. Por lo tanto es biyectiva.

(Pero no desde el conjunto de todos los números reales porque podrías tener por ejemplo

• f(2)=4 y
• f(-2)=4)

FUNCIÓN CRECIENTE 
Una función y=f(x)  es  creciente cuando al aumentar la variable independiente, x, aumenta la variable dependiente, y.

• Una función y=f(x) es decreciente cuando al aumentar la variable independiente, x, disminuye la variable dependiente, y.
• 
  

FUNCIÓN CONSTANTE  

• Una función y=f(x) es constante cuando al aumentar la variable independiente, x, la variable dependiente, y, no varía.
• 
  

FUNCIÓN LINEAL 

Sea A y  B Números reales , la función F de R en R  cuya regla de correspondencia es f(x)=ax+b.

Ejemplo

función monótona

En matemáticas, una función entre conjuntos ordenados se dice monótona (o isótona) si conserva el orden dado. Las funciones de tal clase surgieron primeramente en cálculo, y fueron luego generalizadas al entorno más abstracto de la teoría del orden. Aunque los conceptos generalmente coinciden, las dos disciplinas han desarrollado una terminología ligeramente diferente; mientras en cálculo se habla de funciones monótonamente crecientes y monótonamente decrecientes (o simplemente crecientes y decrecientes), en la teoría del orden se usan los términos monótona y antítona, o se habla de funciones que conservan e invierten el orden.

función par

Una función par es cualquier función que satisface la relación f(x) = f(-x)\, y si x es del dominio de f entonces -x también.

Desde un punto de vista geométrico, una función par es simétrica con respecto al eje y, lo que quiere decir que su gráfica no se altera luego de una reflexión sobre el eje y.

Ejemplos de funciones pares son el valor absoluto, x2, x4, cos(x), y cosh(x).

Una función impar es cualquier función que satisface la relación:

   f(-x) = -f(x)\,

para todo x en el dominio de f.

función impar

Desde un punto de vista geométrico, una función impar posee una simetría rotacional con respecto al origen de coordenadas, lo que quiere decir que su gráfica no se altera luego de una rotación de 180 grados alrededor del origen.

Ejemplos de funciones impares son x, x3, seno(x), sinh(x), y la erf (x).

función es periódica

En matemática, una función es periódica si los valores de la función se repiten conforme se añade a la variable independiente un determinado período, es decir:

f \left ( x \right ) = f \left ( x + P \right )

donde P es el período.

De la misma manera, pero en un contexto físico, las ondas periódicas son aquellas ondas que muestran periodicidad respecto del tiempo,es decir, describen ciclos repetitivos. En una onda periódica se cumple:

x_a (t) = x_a (t+T_p) = x_a (t+nT_p) \,\!

donde el periodo propio fundamental T_p = \frac {1}{F} \,\!, F \,\! es la frecuencia de la componente fundamental de la onda periódica y n \,\! un número entero.

Toda onda periódica es, por definición, una onda determinista, por cuanto puede ser descrita matemáticamente (mediante un modelo matemático)

función definida a trozos

En matemáticas, una función definida a trozos (también denominada función por partes, función seccionada o función definida por tramos) es una función cuya definición (la regla que define la dependencia), llamada regla de correspondencia, cambia dependiendo del valor de la variable independiente.1

Gráfica de una función

Formalmente, una función real f (definida a trozos) de una variable real x es la relación cuya definición está dada por varios conjuntos disjuntos de su dominio (conocidos como subdominios)

En matemáticas, la gráfica de una función:

   

Es el conjunto formado por todos los pares ordenados (x, f(x)) de la función f, es decir, como un subconjunto del producto cartesiano X×Y. Se representa gráficamente mediante una correspondencia entre los elementos del conjunto dominio y los del conjunto imagen.

Las únicas funciones que se pueden trazar de forma completa son las de una sola variable, con un sistema de coordenadas cartesianas, donde cada abscisa representa un valor de la variable del dominio y cada ordenada representa el valor correspondiente del conjunto imagen. Si la función es continua, entonces la gráfica formará una línea recta o curva.

En el caso de funciones de dos variables es posible visualizarlas de forma unívoca mediante una proyección geométrica, pero a partir de tres variables tan solo es posible visualizar cortes (con un plano) de la función para los que los valores de todas las variables, excepto dos, permanezcan constantes.

El concepto de gráfica de una función se generaliza a la gráfica de una relación. Notar que si bien cada función tiene una única representación gráfica, pueden existir varias funciones que tengan la misma, pero con dominios y codominios diferentes.

OPERACIONES CON FUNCIONES

Suma de funciones

Sean f  y g dos funciones reales de variable real definidas en un mismo intervalo. Se llama suma de ambas funciones, y se representa por f + g, a la función definida por

                                           

Resta de funciones

Del mismo modo que se ha definido la suma de funciones, se define la resta de dos funciones reales de variable real f y g, como la función

                                           

Para que esto sea posible es necesario que f y g estén definidas en un mismo intervalo.

Producto de funciones

Sean f y g dos funciones reales de variable real, y definidas en un mismo intervalo. Se llama función producto de f y g a la función definida por

                                           

Cociente de funciones

Dadas dos funciones reales de variable real, f y g, y definidas en un mismo intervalo, se llama función cociente de f y g a la función definida por

                                                 

(La función f/g está definida en todos los puntos en los que la función g no se anula.)

Producto de un número por una función

Dado un número real a y una función f, el producto del número por la función es la función definida por

                                              

APLICACIONES