RESEÑA HISTORICA
El primero en usar los números complejos fue el matemático italiano Girolamo Cardano (1501–1576) quien los usó en la fórmula para resolver las ecuaciones cúbicas. El término “número complejo” fue introducido por el gran matemático alemán Carl Friedrich Gauss (1777–1855) cuyo trabajo fue de importancia básica en álgebra, teoría de los números, ecuaciones diferenciales, geometría diferencial, geometría no euclídea, análisis complejo, análisis numérico y mecánica teórica, también abrió el camino para el uso general y sistemático de los números complejos.
Los números complejos
Los números complejos son una extensión de los números reales y forman el mínimo cuerpo algebraicamente cerrado que los contiene. El conjunto de los números complejos se designa con la notación

, siendo

el conjunto de los números reales se cumple que

(

está estrictamente contenido en

). Los números complejos incluyen todas las raíces de los polinomios, a diferencia de los reales. Todo número complejo puede representarse como la suma de un número real y un número imaginario (que es un múltiplo real de la unidad imaginaria, que se indica con la letra
i), o en forma polar.
Los números complejos son la herramienta de trabajo del álgebra,
análisis, así como de ramas de las matemáticas puras y aplicadas como
variable compleja, ecuaciones diferenciales, facilitación de cálculo de
integrales, en aerodinámica, hidrodinámica y electromagnetismo entre
otras de gran importancia. Además los números complejos se utilizan por
doquier en matemáticas, en muchos campos de la física (notoriamente en la mecánica cuántica) y en ingeniería, especialmente en la electrónica y las telecomunicaciones, por su utilidad para representar las ondas electromagnéticas y la corriente eléctrica.
En matemáticas, estos números constituyen un cuerpo y, en general, se consideran como puntos del plano: el plano complejo.
Este cuerpo contiene a los números reales y los imaginarios puros. Una
propiedad importante que caracteriza a los números complejos es el teorema fundamental del álgebra — pero que se demuestra aún en un curso de variable compleja —, que afirma que cualquier ecuación algebraica de grado
n tiene exactamente n soluciones complejas. Los análogos del cálculo diferencial e integral con números complejos reciben el nombre de variable compleja o análisis complejo.
UNIDAD IMAGINARIA
En matemáticas, un
número imaginario es un número complejo cuya parte real es igual a cero, por ejemplo:

es un número imaginario, así como
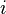
o

son también números imaginarios. En otras palabras, es un número de la forma:
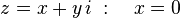
Un número imaginario puede describirse como el producto de un número real por la
unidad imaginaria i, en donde la letra
i denota la raíz cuadrada de -1 :
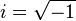
Fue en el año 1777 cuando Leonhard Euler le dio a

el nombre de
i, por imaginario, de manera despectiva dando a entender que no tenían una existencia real. Gottfried Leibniz, en el siglo XVII, decía que

era una especie de anfibio entre el ser y la nada.
En ingeniería eléctrica y campos relacionados, la unidad imaginaria es a menudo escrita como
j para evitar la confusión con la intensidad de una corriente eléctrica, tradicionalmente denotada por
i.
FORMA VECTORIAL DE NUMEROS COMPLEJOS
Ahora que sabemos trabajar con los números complejos y las
operaciones básicas de suma, resta, multiplicación y división, vamos a
introducirnos en la representación de dichos números en el plano
complejo. Para los números reales, dibujábamos una recta y los íbamos
colocando ordenadamente, es decir:

Para representar gráficamente un número complejo, debemos dibujarlos
en el plano complejo. Éste está formado por un eje real y un eje
imaginario. Sobre el eje real representaremos la parte real del número
complejo, mientras que en el eje imaginario representaremos la parte
imaginaria. Dichos ejes los dibujaremos perpendiculares y secantes en el
cero, que tiene parte real e imaginaria nula.
Ejemplo
Veamos un ejemplo del plano complejo:

Un número complejo
z en forma binómica se representará entonces en un plano complejo como el anterior de la siguiente forma:
Tenemos el complejo
z=a+bi donde:
- a es cualquier número real, y se le llama parte real de z.
- b es cualquier número real, y se le llama la parte imaginaria de z.
Así, para representar un
z=a+bi se dibuja en el plano el vector asociado a
z que es el vector con origen
(0,0) y extremo el punto
(a,b).
Es decir, se toma la parte real del complejo y se dibuja en el eje
real.
Se toma la parte imaginaria y se dibuja en el eje imaginario.
Se trazan paralelas a los ejes que pasen por cada uno de los puntos
marcados y la intersección de dichas paralelas es el número que
queríamos representar.

Ejemplo
Por ejemplo, si queremos representar el imaginario
z=2−i.
Primero marcamos en el eje real el
2.
Luego marcamos en el eje imaginario el
−i.
Trazamos dos rectas:
- una paralela al eje real que pase por el punto −i.
- una paralela al eje imaginario que pase por el punto 2.
El punto intersección de estas dos rectas es el número z que queríamos dibujar.
Gráficamente es:

En definitiva lo que estamos haciendo es que a cada número complejo que viene dado por la forma
z=a+bi le asociamos un vector en el plano que es exactamente el vector
(a,b).
Ejemplo
Por ejemplo, el complejo 3+9i es el asociado al vector del plano (3,9) y el complejo −5i es el asociado al vector (0,−5).
Anteriormente hemos dicho que:
Se define el conjugado de un número imaginario como el número
z¯=a−ib, en este caso, para representarlo tomaremos el vector asociado
(a,−b).
El opuesto de un número imaginario es
zop=−z=−a−bi, que tendrá vector asociado el
(−a,−b).
Y el inverso de un número complejo es
z−1=aa2+b2−ba2+b2i que tendrá vector asociado el
(aa2+b2,−ba2+b2).
Si los dibujamos en el plano complejo estos quedan:
Conjugado de un Numero Complejo
Se llama conjugado de un número complejo al número complejo que se obtiene por simetría del dado respecto del eje de abscisas.
Representando el número complejo a + bi y haciendo la correspondiente simetría, se tiene que su conjugado es a - bi .
Dado un número complejo, su conjugado puede representarse poniendo encima del mismo una línea horizontal.
Dado un número complejo (x,y) el complejo conjugado sería (x,-y).
Si
al número complejo lo representamos por n; n = (x ,y) el complejo
conjugado se representa por n; n = (x ,-y) con una raya encima del
número.
Propiedades de los Conjugados
· Primera propiedad
El conjugado del conjugado de un complejo z es el propio z.
Demostración:
si z = a + bi se tiene que = a - bi , de donde, = a + bi = z
· Segunda propiedad
Dados dos números complejos cualesquiera z y z' , el conjugado de su suma es igual a la suma de sus conjugados.
Demostración:
Tomando : z = a + bi y z' = c + di
Se obtiene:
a + bi y ' = c - di
Con lo que:
(a + bi ) + (c - di ) = (a + c) + (-b - d)i
· Tercera propiedad
El conjugado del producto de dos números complejos es igual al producto de los conjugados de dichos números:
Demostración:
Si z = a + bi y z = c + di
Se tiene que z · z = (ac - bd ) + (ad + bc)i
Cuyo conjugado es (ac - bd) - (ad + bc)i .
Calculando por otro lado el producto de los conjugados, resulta que
(a - bi )( c - di ) = ( ac - bd ) + ( -ad - bc) i .
· Cuarta propiedad
Los complejos que coinciden con sus conjugados son los números reales.
Demostración:
Sea un complejo a + bi que coincida con su conjugado.
Esto equivale a que:
a + bi = a - bi
Pero esto sólo ocurre si b = 0, es decir si a + bi es un número real.
· Quinta propiedad
La suma y el producto de un complejo y su conjugado son, ambos, números reales.
Demostración: (a + bi ) + (a - bi ) = 2a
(a + bi ) (a - bi ) = a2 - (bi )2 = a2 + b2
Complejo opuesto
Dado un número complejo (x,y) el complejo opuesto sería (-x,-y)
Si al número complejo lo representamos por n, el complejo opuesto se representa por n'.
Si z = a +b
i
El opuesto de z seria -z = -a - b
El Conjugado de z seria z = a + bi
 OPERACIONES
OPERACIONES
Igualdad
Dos números complejos son iguales cuando sus partes reales y sus partes imaginarias son iguales entre sí.
a + bi = c + di quiere decir a = c y b = d
Ejemplo:
Determina para qué valores de x e y son iguales los números complejos: z = x -3 + 5i,
w = 4 + (y + 4)i
Igualamos por separado las partes reales x -3 =4 y se obtiene x =7 y las partes imaginarias
5 = y + 4, se obtiene y = 1.
Luego para que sean iguales debe cumplirse que x = 7 e y = 1.
Operaciones con Números Complejos
Suma de Números Complejos
Dados dos números complejos a + bi y c + di se definen su suma como:
(a + bi ) + (c + di ) = (a + c) + (b + d)i
Propiedades de la Suma de Números Complejos
La suma de números complejos tiene las siguientes propiedades:
· Conmutativa
Dados dos números complejos a + bi y c + di se tiene la igualdad:
(a + bi ) + (c + di ) = (c + di ) + (a + bi )
Ejemplo:
(2 - 3i ) + (-3 + i ) = (2 - 3) + i (-3 + 1) = -1 - 2i
(-3 + i ) + (2 - 3i ) = (-3 + 2) + i (1 - 3) = -1 - 2i
· Asociativa
Dados tres complejos a + bi, c + di y e + fi , se cumple:
[(a + bi ) + (c + di )] + (e + fi ) = (a + bi ) + [(c + di ) + (e + fi )]
Ejemplo:
[(5 + 2i ) + (3 - 4i )] + (-9 + 8i ) = (8 - 2i ) + (-9 + 8i ) = -1 + 6i
(5 + 2i ) + [(3 - 4i ) + (-9 + 8i )] = (5 + 2i ) + (-6 + 4i ) = -1 + 6i
· Elemento neutro
El elemento neutro es 0 + 0i , puesto que
(a + bi ) + (0 + 0i ) = (a + 0) + i (b + 0) = a + bi
El número 0 + 0i se escribe simplificadamente 0 y se le llama «cero».
· Elemento simétrico
El elemento simétrico de un número complejo cualquiera a + bi es (- a - bi ):
(a + bi ) + (-a - bi) = 0 + 0i = 0
Ejemplo:
El simétrico de 2 - 3i es -2 + 3i pues (2 - 3i ) + (-2 + 3i ) = 0
Producto de Números Complejos
La multiplicación se
efectúa igual que si fuesen números reales, pero teniendo en cuenta que
la multiplicación de complejos no es equivalente al producto escalar de
vectores.
Dados dos números complejos a + bi y c + di se definen su producto como:
(a + bi ) (c + di ) = (ac - bd) + (ad + bc)i
El producto puede hacerse operando con i como si fuese un número real y teniendo en cuenta que i 2 = -1.
(a + bi )(c + di ) = ac + adi + bci + bdi 2 = ac + i(ad + bc) + bd(-1) = ac - bd + i (ad + bc)
Pero
para comprobar resultados, podemos representar los complejos que se
multiplican por sus vectores, y el resultado del producto por el vector
correspondiente al complejo producto.
Propiedades del Producto de Complejos
· Conmutativa
Dados dos complejos a + bi y c + di , se cumple que:
(a + bi ) (c + di ) = (c + di ) (a + bi )
· Asociativa
Dados los complejos a + bi, c + di y e + fi se cumple que:
[(a + bi ) (c + di )](e + fi ) = (a + bi ) [(c + di ) (e + fi )]
· Elemento neutro
El
elemento neutro del producto es 1 + 0 ·i = 1, puesto que para cualquier
complejo a + bi , (a + bi ) (1 + 0 · i ) = (a + bi ) · 1 = a + bi . El
elemento neutro es el uno.
· Distributiva del producto con respecto a la suma
Dados tres números complejos a + bi , c + di y e + fi , se cumple:
(a + bi ) [(c + di ) + (e + fi )] = (a + bi ) (c + di ) + (a + bi ) (e + fi )
Ejemplo:
(1 - 2i ) [3i + (2 - 7i )] = (1 - 2i ) (2 - 4i ) = 2 - 4i - 4i + 8i 2 = -6 - 8i
(1 - 2i ) 3i + (1 - 2i ) (2 - 7i ) = (3i - 6i 2) + (2 - 7i - 4i + 14i 2) = (3i + 6) + (-12 - 11i )
= - 6 - 8i
El
conjunto de los números complejos, por contar con todas las propiedades
anteriores para la suma y para el producto, se dice que es un anillo
conmutativo.
El conjunto de los números complejos se simboliza por C, o también (C, +, ·).
· Elemento simétrico respecto del producto
Dado
un complejo cualquiera a + bi , distinto de 0 + 0i , existe otro
complejo que, multiplicado por él, da el elemento neutro del producto,
es decir, 1 + 0i .
Demostración:
Se intentará calcular el inverso de a + bi , x + yi .
Ha de verificarse que (a + bi ) (x + yi ) = 1 + 0i
(a + bi ) (x + yi ) = (ax - by) + (ay + bx)I
Por tanto ha de ser:
ax - by = 1, multiplicando por a se tiene: a2x - aby = a
bx + ay = 0, multiplicando por b se tiene: b2x + aby = 0
El conjunto de los números complejos es un cuerpo conmutativo con la suma y el producto definidos.
División de números complejos en forma binómica
Para dividir números complejos en
forma binómica se multiplica numerador y denominador por el conjugado
del denominador y se realizan las operaciones correspondientes.
División de números complejos en forma polar
La división de dos números complejos es otro número complejo tal que:
Su módulo es el cociente de los módulos.
Su argumento es la diferencia de los argumentos.
645° : 315° = 230°
 tiene la forma:
tiene la forma:Mm,n

 , con
, con

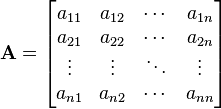
 , siendo
, siendo  el conjunto de los números reales se cumple que
el conjunto de los números reales se cumple que  (
( es un número imaginario, así como
es un número imaginario, así como 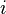 o
o  son también números imaginarios. En otras palabras, es un número de la forma:
son también números imaginarios. En otras palabras, es un número de la forma: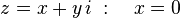
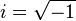
 el nombre de i, por imaginario, de manera despectiva dando a entender que no tenían una existencia real. Gottfried Leibniz, en el siglo XVII, decía que
el nombre de i, por imaginario, de manera despectiva dando a entender que no tenían una existencia real. Gottfried Leibniz, en el siglo XVII, decía que 

