RESEÑA HISTORICA
El origen de las matrices es muy antiguo. Los cuadrados latinos y los cuadrados mágicos se estudiaron desde hace mucho tiempo. Un cuadrado mágico, 3 por 3, se registra en la literatura china hacia el 650 a. C.
Es larga la historia del uso de las matrices para resolver ecuaciones lineales. Un importante texto matemático chino que proviene del año 300 a. C. a 200 a. C., Nueve capítulos sobre el Arte de las matemáticas (Jiu Zhang Suan Shu), es el primer ejemplo conocido de uso del método de matrices para resolver un sistema de ecuaciones simultáneas. En el capítulo séptimo, "Ni mucho ni poco", el concepto de determinante apareció por primera vez, dos mil años antes de su publicación por el matemático japonés Seki Kōwa en 1683 y el matemático alemán Gottfried Leibniz en 1693.
Los "cuadrados mágicos" eran conocidos por los matemáticos árabes, posiblemente desde comienzos del siglo VII, quienes a su vez pudieron tomarlos de los matemáticos y astrónomos de la India, junto con otros aspectos de las matemáticas combinatorias. Todo esto sugiere que la idea provino de China. Los primeros "cuadrados mágicos" de orden 5 y 6 aparecieron en Bagdad en el 983, en la Enciclopedia de la Hermandad de Pureza (Rasa'il Ihkwan al-Safa).
Después del desarrollo de la teoría de determinantes por Seki Kowa y Leibniz para facilitar la resolución de ecuaciones lineales, a finales del siglo XVII, Cramer presentó en 1750 la ahora denominada regla de Cramer. Carl Friedrich Gauss y Wilhelm Jordan desarrollaron la eliminación de Gauss-Jordan en el siglo XIX.
Fue James Joseph Sylvester quien utilizó por primera vez el término « matriz » en 1848/1850.
En 1853, Hamilton hizo algunos aportes a la teoría de matrices. Cayley introdujo en 1858 la notación matricial, como forma abreviada de escribir un sistema de m ecuaciones lineales con n incógnitas.
Cayley, Hamilton, Hermann Grassmann, Frobenius, Olga Taussky-Todd y John von Neumann cuentan entre los matemáticos famosos que trabajaron sobre la teoría de las matrices. En 1925, Werner Heisenberg redescubre el cálculo matricial fundando una primera formulación de lo que iba a pasar a ser la mecánica cuántica. Se le considera a este respecto como uno de los padres de la mecánica cuántica.
CLASES DE MATRICES
DEFINICION En matemática, una matriz es un arreglo bidimensional de números. Dado que puede definirse tanto la suma como el producto de matrices, en mayor generalidad se dice que son elementos de un anillo. La notacion de una matriz
 tiene la forma:
tiene la forma:Las matrices se utilizan para múltiples aplicaciones y sirven, en particular, para representar los coeficientes de los sistemas de ecuaciones lineales o para representar transformaciones lineales dada una base. En este último caso, las matrices desempeñan el mismo papel que los datos de un vector para las aplicaciones lineales.
Pueden sumarse, multiplicarse y descomponerse de varias formas, lo que también las hace un concepto clave en el campo del álgebra lineal.
CLASIFICACIÓN Y PROPIEDADES DE LAS MATRICES
- IGUALDAD ENTRE MATRICESDos matrices son iguales si tienen las mismas dimensiones y cada elemento de la primera es igual al elemento de la segunda que ocupa su misma posición. Es decir:
Mm,n
- POTENCIAS DE MATRICES CUADRADAS
En este capítulo vamos a tratar de exponer distintas técnicas
para hallar las potencias naturales de matrices cuadradas. Esta cuestión es de
gran importancia y tiene muchas aplicaciones prácticas. Como vamos a poder
observar el cálculo de potencias de matrices cuadradas lleva consigo un número
muy elevado de operaciones. Es conveniente encontrar estrategias adecuadas
que nos permitan calcular de modo eficiente las potencias naturales de matrices
cuadradas
DETERMINANTE
Determinantes de una matriz
Dada una matriz cuadrada

se llama determinante de A, y se representa por |A| ó det(A), al número:
 , con
, con
(Sn es el grupo de las permutaciones del conjunto {1, 2,.. n}, e i(s) es la signatura de la permutación)
También se suele escribir:

Dada una matriz cuadrada
se llama determinante de A, y se representa por |A| ó det(A), al número:
También se suele escribir:
MÉTODOS PARA ENCONTRAR LA DETERMINANTE DE UNA MATRIZ
El
determinante de una matriz suele utilizarse con frecuencia en
operaciones de cálculo, álgebra lineal y geometría descriptiva a
un nivel más complejo. Fuera del mundo académico, los ingenieros y
los programadores gráficos utilizas las matrices y sus determinantes
constantemente.Si sabes cómo hallar el determinante de una matriz de
2x2, las únicas herramientas que tendrás que utilizar serán la
suma, la resta y la multiplicación.
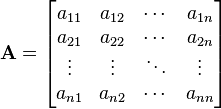
No hay comentarios:
Publicar un comentario